Who doesn’t love a game of chance? One of my favourite days of the year is ANZAC Day as it means I get to play two up. Every week I play another game of chance as a bonus round at Trivia which seems like it might be possible to get an advantage in unlike other games of chance.

The game is Heads & Tails and it is about as simple as it gets: you pick heads or tails, a coin is flipped and everyone who picks wrong sits down. This repeats until there is just one left. At the surface, this seems just like any other game of chance except that you are not an indivual when you play trivia, you are part of a team. As you don’t need to win as an individual to reap the rewards, maybe there is some strategy that gives your team a slight edge that will get you a victory more often than the rest.

To figure this out im sure you could calculate the probabilities and for all the different strategies but I was never very good at probability calculations so I did the lazy things and simulated millions of games to just get the answer.

Strategies

The two most obvious strategies are to choose randomly and to split the team fifty/fifty to ensure that at least one person progresses to the next round. We can treat these as the baseline strategies to compare any strategies against as these represent the least strategic strategy (random) and the minimum guaranteed win for a given team size (fifty/fifty).

It turns out that coming up with creative strategies is difficult in a game with a very small set of possible choices (or maybe I am not capabable of a big brain strat). As a result, we are not looking at many other strategies as I could only come up with:

1. Random
2. Fifty/fifty
3. All same every round
4. All same in a given round
5. Some combination of these

Random vs Fifty/Fifty

The first burning question is whether one of our baseline strategies is better than the other. So to find out, I made 18 teams of six players each play 500,000 games of heads of tails where half would use a random strategy and half fifty/fifty. From this it seems like there is no overall benefit between these strategies for similarly sized teams.

Effect of Team Size

Of course team size is not always the same. Some teams will alwayse have more members than others and a bigger feels like it will be better in this case. But, as I man of science, I cannot let a feeling go untested.

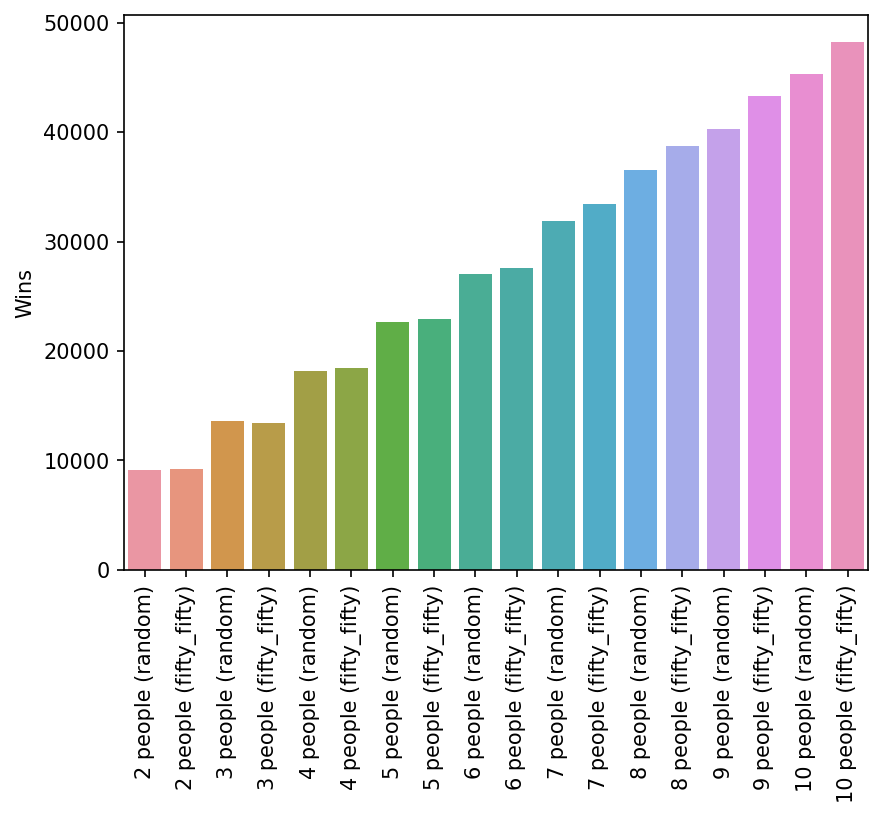
Looks like the gut was right this round. The easiest way to increase your chances of winning is to invite an extra friend.

However, there is something interesting in this data which shows that the choice of splitting fifty/fifty and going random depends on team size. If your team has less than five people, your best strategy is to go randomly. If you have seven or more people then the best strategy is go fifty/fifty. For team sizes of five or six, it is about the same.

Going All The Same

Now for the big question: can going all the same give you an edge?

Intuitively, it seems like this strategy can give you an edge as long as you don’t use it throughout the whole game. If you do that, you will lose most of the time.

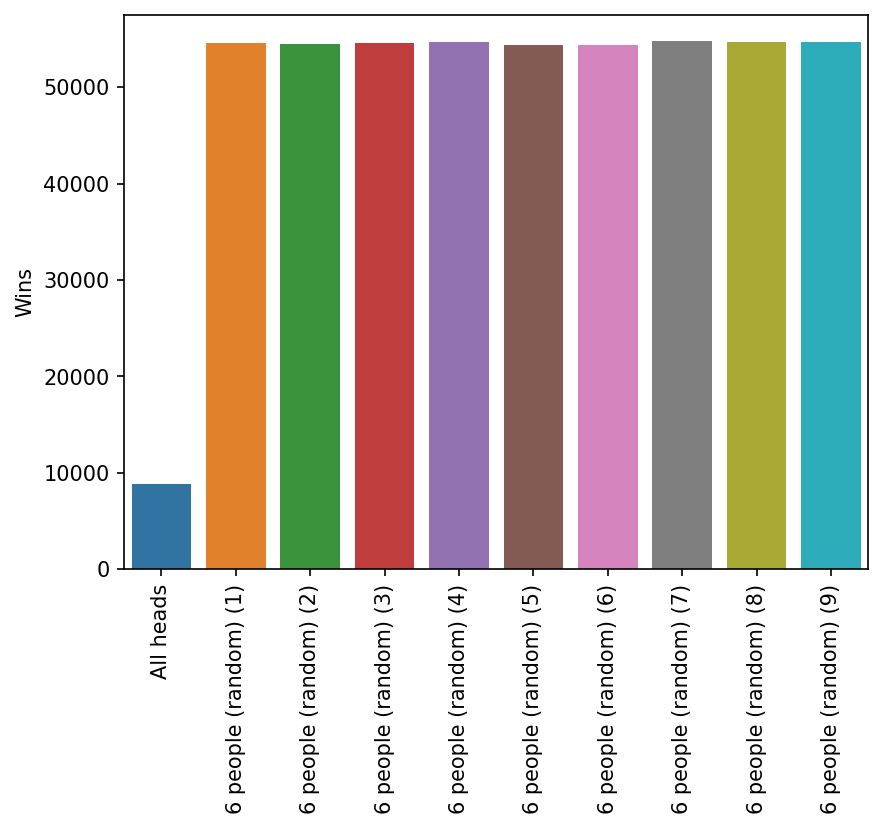
All Same First Round

But what about just for the first round? Does the benefit of having all players in the second round half the time balance out being all out half the time?

Of course the answer is “it depends” as these strategies don’t exist in a vacuum, the exist against other strategies so lets see how this strategy fairs against nine other teams of the same size.

The above graph shows the result of 500,000 games of ten teams with six players each where one team goes all the same in the first round and then chooses randomly there after (the same strategy as the rest of the teams). Inerestingly, this appears to be a bad strategy - you will lose more often doing this.

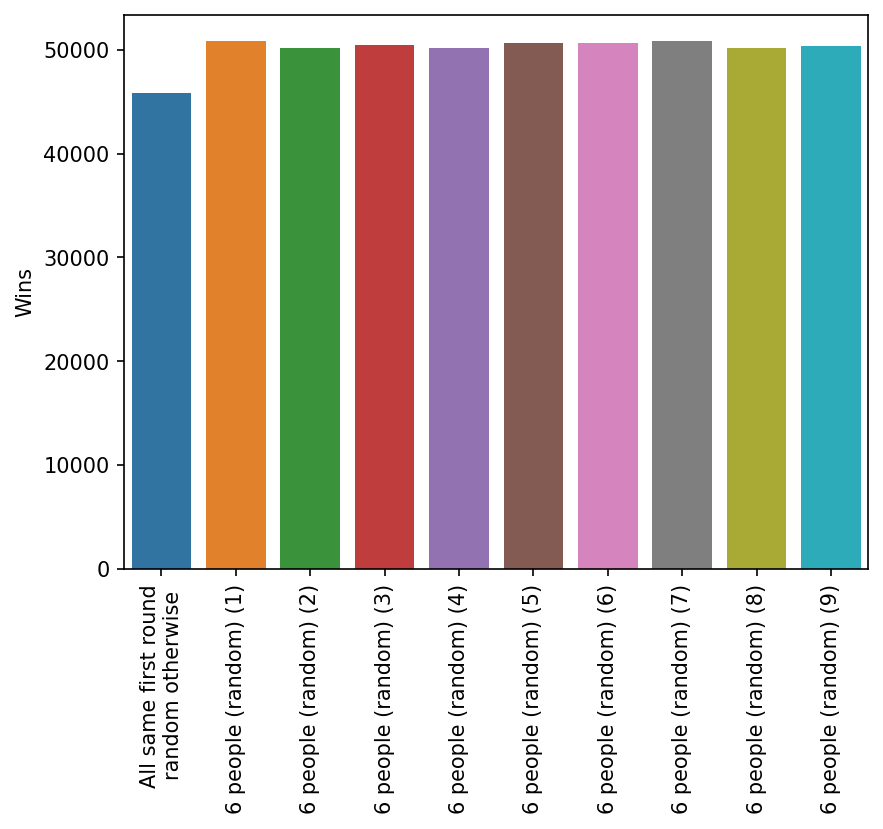
However, if you split fifty/fifty after the first round, this appears to give you an advantage.

And this advantage is retained even when all the other teams employ the fift/fifty strategy too, showing that there is a real advantage to going all the same in the first round as long you split fifty/fifty afterwards.

I interpret this to mean that going the same in the first round and winning is effetively like doubling your team size for that game which obviously would give you a large advantage over a similarly sized team. What isn’t obvious is that this is not balanced out by all the times you lose.

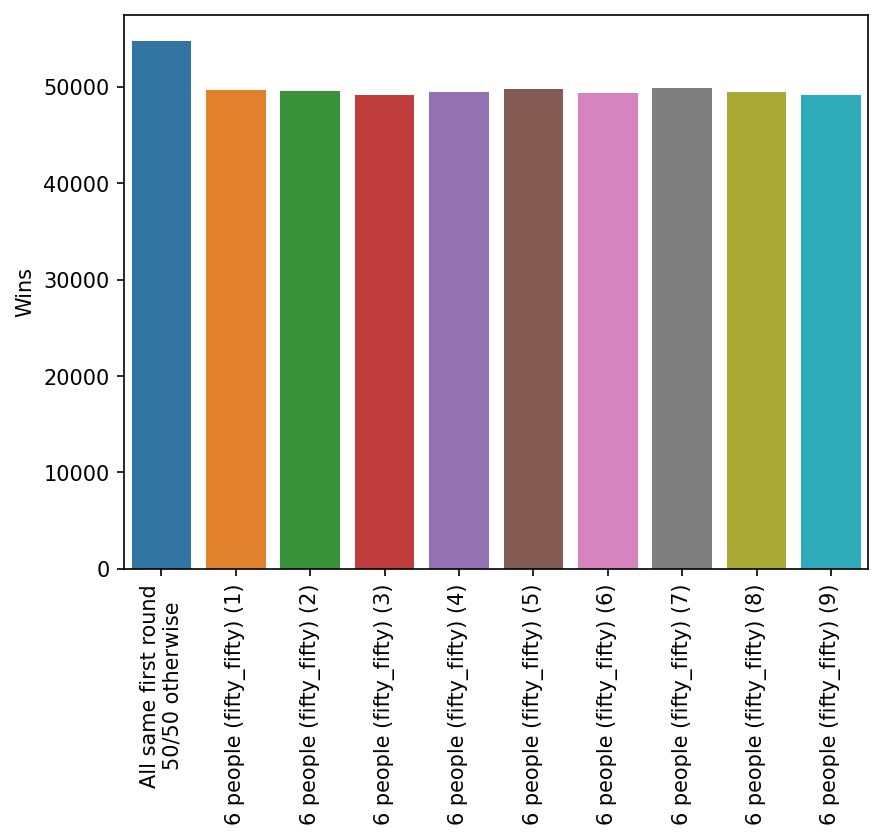
All Same in Later Rounds

If this is a legetimate strategy, is it better to continue it and go all the same in multiple rounds? Is there something about the first round that makes it special or can you go all the same in the second round instead? Let’s answer the second quesion first

It turns out yes, going all the same in the second round still has a benefit over just going fifty/fifty. This suggests the team doubling effect works in a later round too.

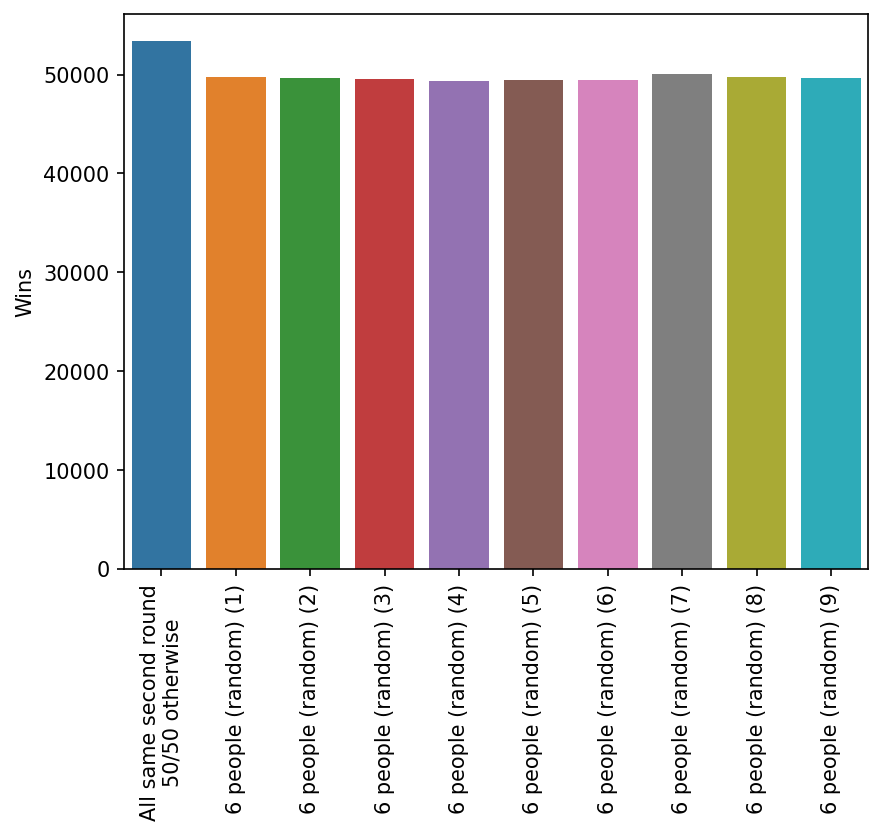
This is true for the third round too.

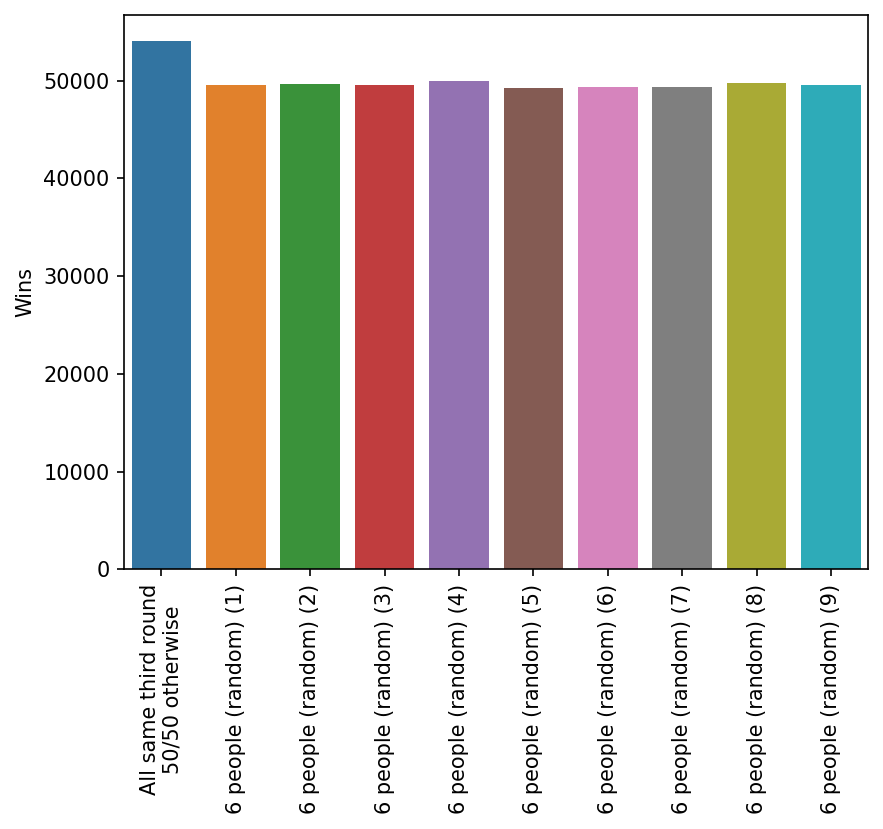
Going all the same in one round is good. So going all the same in two rounds should be even better, right? Wrong. Turns out that is a bad strategy. Here the risk clearly does outwiegh the reward.

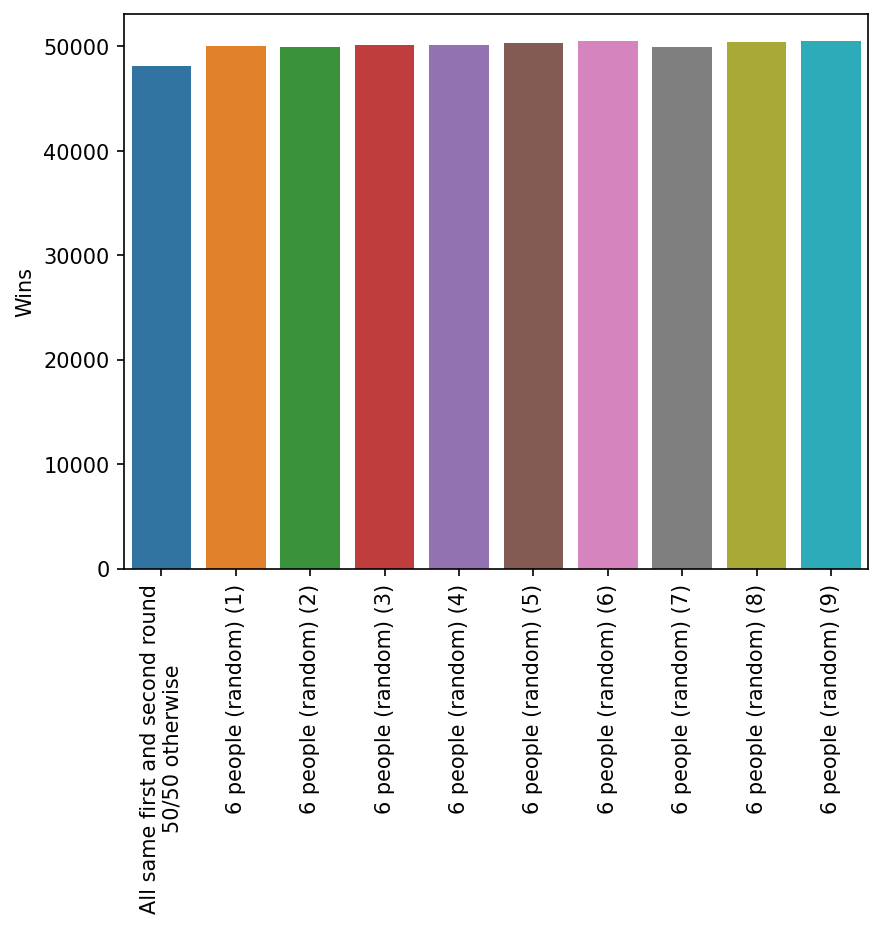
Putting It All Together

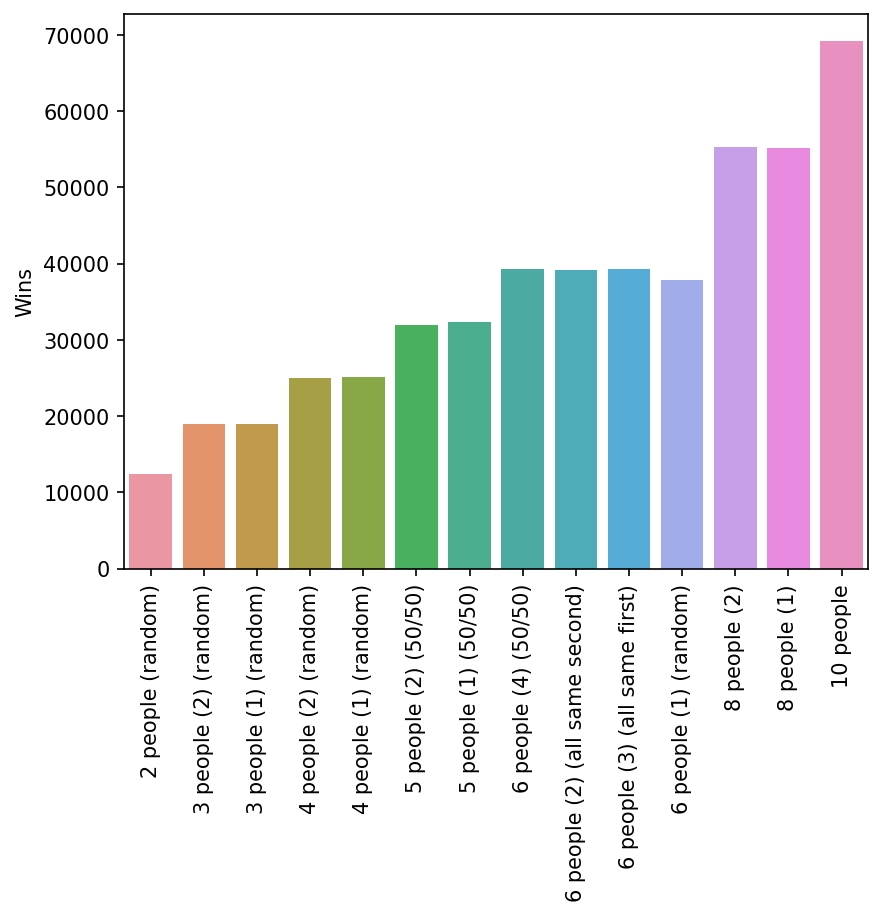
Now we have an idea about the best strategy to win the game, lets simulate some more realisitic games and see how having teams of different sizes changes the result.

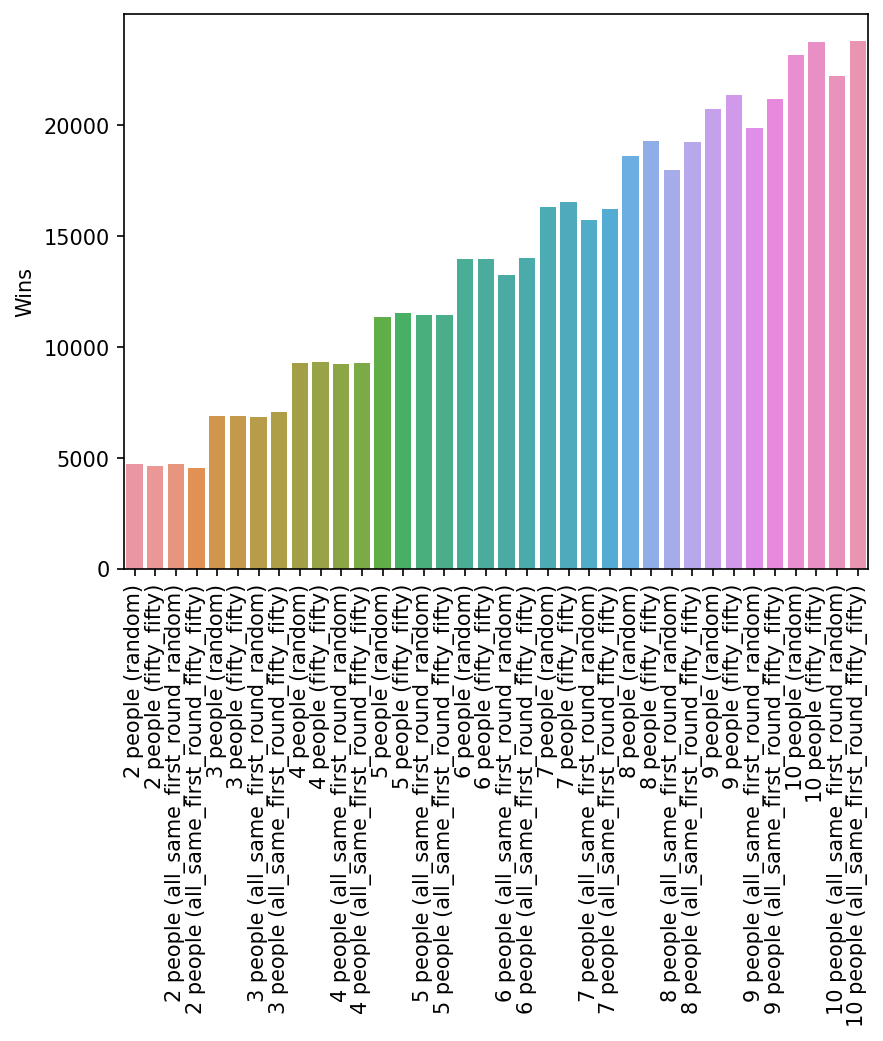
The relative advanatage of going all the same in the first round doesn’t propagate when there are larger teams. This is surprising to me as I would have thought that having an advantage over teams of the same size would translate into relatively more victories against larger teams.

To finish this off, let’s look at a more “realisitic” simulation with a mix of teams of different sizes somewhat similar to what you might see at the pub on a Tuesday night with most teams having between 4-6 people. Again, it seems the only real advantage is having more team members.

Key Take Aways

1. A bigger team will win more often
2. For teams less than five people a picking randomly is better than splitting 50/50
3. For teams with seven or more people, splitting 50/50 is better than picking randomly
4. Going all the same in a round gives you a relative advantage as long as you go split the rest of the time (for a team of six people)
5. The relative advantage due to going all the same in the first round doesn’t translate to more victories for a smaller team.

See github for the code used in this post.